An introduction to cryptographic techniques
Cryptography is one of the essential technologies used in building a secure VPN. Different applications of the same basic algorithms can provide both encryption that keeps data secret and authentication that ensures the two security peers in a VPN are who they claim to be. This chapter introduces some basic concepts in cryptography and demonstrates how they can be used in practice to provide data confidentiality. The next chapter continues this theme with a discussion of mutual authentication using cryptographic algorithms.
Data confidentiality may be provided by one of two categories of encryption algorithm, namely symmetric cryptography and asymmetric cryptography. Symmetric, or conventional, cryptography requires that the sender and receiver share a key, which is an item of secret information used to encrypt and decrypt data. The process by which two peers agree upon a key over an insecure medium can be problematic as, until the key is agreed, the peers have no way to communicate in secret. Asymmetric, or Public Key, cryptography solves the key exchange problem by using two keys, either of which may be used to encrypt a message. The encrypted data may then only be decrypted by means of the other key. Messages may be received securely by publishing one of the keys (for example, in the footer of an e-mail message) as a Public Key and keeping the second, the Private Key, secret. Anyone wishing to send a secure communication may then encrypt the message with the recipient’s Public Key and, providing the Private Key has not been disclosed, only the intended recipient will be able to decrypt the encrypted text and recover the original message.
Throughout this discussion, the original unencrypted data will be referred to as plaintext and the encrypted form as ciphertext.
Symmetric Ciphers
Symmetric ciphers employ the same key to encrypt the plaintext and to decrypt the ciphertext. The sender and the recipient must therefore agree upon this key, which must be known to no one else, in advance. The cryptographic strength of a symmetric algorithm may be gauged by the size of the key it employs. The examples are DES (Data Encryption Standard), Blowfish, and AES. The DES algorithm uses a 64-bit key, of which 8 bits are reserved leaving 56 variable bits. It is possible to protect information with 3DES (Triple DES) instead of DES. This means that the information is subjected to three successive encryptions. The use of multiple encryption cycles does not necessarily offer a concomitant increase in security, and may be viewed as a waste of computing power for many applications. Blowfish allows implementers to select a key length of between 32 and 448 bits; commercially available implementations often use 128-bit keys. In 2002 DES was replaced by AES as an encryption standard by the US government [3]. Since then AES has become very popular because it combines the speed of DES with the security level of Triple DES. AES can use 128, 192 and 256-bit keys; many public AES-based products use 128-bit secret keys by default.
Symmetric algorithms are popular because their speed enables them efficiently to encrypt large quantities of plaintext. There are two subcategories of symmetric cipher, stream and block ciphers.
Stream Ciphers
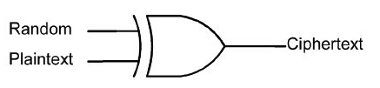
These algorithms operate upon one bit at a time. A stream of plaintext flows into the cipher and a stream of ciphertext emerges as the output. Messages encrypted with a stream cipher are always the same size as the original plaintext. The encryption takes place by means of an operation in which each bit of the plaintext is XORed (i.e. manipulated by the Boolean operator eXclusive OR – XOR) with a random bit to produce the ciphertext. The essence of a stream cipher concerns the methods by which the shared key is used to generate the stream of random bits. Cracking attempts centre on analysing this random bit generator (Figure 1).
Figure 1. Random bit generator
Block Ciphers
These ciphers encrypt data in blocks of bytes, rather than a single bit at a time. Block sizes vary according to the algorithm, 64 bits being the commonest. Because the plaintext is unlikely to be a multiple of the algorithm’s block size, it is often necessary to pad the input. For example, if the block length is 64 bits and the last block contains only 40 bits then 24 bits of padding must be added. The padding string can consist of all zeros, alternating zeros and ones, random bits, or some other sequence. Some encryption standards specify a particular padding scheme. DES, Blowfish and AES are block ciphers.
There are two methods for encrypting a sequence of blocks. Either the blocks are treated independently and the cipher is used on each block without reference to what has gone before, or the results of encrypting previous blocks affect the encryption of the current block. These two methods are known as the ECB (Electronic CodeBook) mode and CBC (Cipher Block Chaining) ciphertext mode respectively.
ECB Mode
In ECB, identical blocks of plaintext will clearly generate identical blocks of ciphertext. A cracker can therefore exploit repetition in the ciphertext to release the plaintext version.
CBC Mode
In CBC, a feedback mechanism is added so that the results of the encryption of previous blocks are fed back into the encryption of the current block. Each ciphertext block is made dependent not only on the plaintext block that generated it, but also on all previous plaintext blocks. This ensures that even if the plaintext contains many identical blocks, they each encrypt to a different ciphertext block. Prior to encryption, CBC takes the last block of ciphertext and XORs it with the current block of plaintext. Although CBC mode forces identical plaintext blocks to encrypt to different
blocks, messages that start with the same data will encrypt in the same way up until the first difference, since the initial plaintext blocks are identical. Encrypting random data, called the Initialisation Vector, as the first block can prevent this. Decryption is the exact opposite in that the ciphertext is decrypted and then XORed with the previous block of ciphertext (or Initialisation Vector for the first block) to release the plaintext version.
Other modes are available but they are not discussed here because all the block ciphers currently used in VPN technology operate exclusively in CBC mode.
Asymmetric Ciphers
As noted in the introduction to this chapter, the great advantage of asymmetric ciphers is that a shared secret key does not have to be exchanged over an insecure medium such as the public Internet. A pair of keys is generated and one of them is nominated as the Public Key and is published. Any parties wishing to communicate securely with the key’s owner encrypt the message using the recipient’s Public Key. The decryption can only be accomplished by knowing the second, Private, key, which the owner ensures is never released.
The most popular asymmetric block cipher is RSA (named after its inventors, Ron Rivest, Adi Shamir, and Leonard Adleman) [4]. The keys of the RSA algorithm are composed of two parts. The first part is called the modulus. It is usually a 512-bit number and is the product of two 256-bit primes.
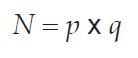
The Public and Private Keys share the same modulus. The second part of an RSA key is called the exponent. This is a variable-length number, different for the two keys, with the exponent of the Public Key usually being the smaller of the two. RSA encryption works as follows. The plaintext (viewed as a binary number) is raised to the power of the Public exponent, and the remainder after dividing by the modulus is the ciphertext. To decrypt, the ciphertext is raised to the power of the Private exponent, and the remainder after dividing by the modulus is the plaintext again. The RSA encryption and decryption functions are as follows:
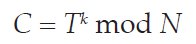
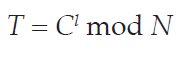
where C is the ciphertext, T is the plaintext, k and l are the public and private exponents and N is the modulus.
The security of asymmetric encryption stems from the difficulty of factoring this modulus back into its constituent primes. Without knowing the two primes used to generate the modulus, it is not possible to calculate the Private exponent from the Public one and therefore an RSA-encrypted message is secure from anyone save the holder of the relevant Private Key.
Key Exchanges
Although the asymmetric encryption algorithms are more secure than the symmetric types, they are also far slower and it is not feasible to use them to secure large quantities of data, as the consequent increase in transmission times would be excessive. Similarly, although chained mode symmetric algorithms can process large quantitiesof plaintext at speed, they do not offer the requisite level of security because the key is a shared secret that must be exchanged over the insecure medium prior to the transmission of the ciphertext. This paradox may be resolved as follows. A random secret, known as the Session Key, is generated and an asymmetric cipher secures this small piece of data for exchange over the Internet. A fast symmetric cipher then uses the Session Key, known only to the two security peers, to encrypt their exchanges of bulk data.
RSA Key Exchange
The RSA algorithm may be employed to provide a simplistic form of secure key exchange. If Alice wishes to secure some large quantity of data with a fast algorithm such as DES before transmitting the data to Bob, she first chooses some random 56-bit number as the DES key and encrypts it using Bob’s RSA Public Key. Only Bob will be able to decrypt this exchange using his private RSA key. The drawback with this approach is that anybody, including the cracker Mallory, can encrypt anything using Bob’s Public Key. Bob therefore has no proof that it is indeed Alice with whom he is communicating. The communications channel is only secure if Alice digitally signs the DES key and encrypts both the key and her signature with Bob’s Public Key. The problem with this approach is that the signature can be too big to secure in a single RSA operation.
Diffie-Hellman Exchange
The Diffie-Hellman key exchange was the first Public Key cryptosystem and it underpins the entire framework by which IP packets may be securely transmitted over the Internet. The participants in the exchange must first agree upon a group, which defines the prime p and generator g that should be used. In the first part of the exchange, Alice and Bob each select a random private number (indicated by the lowercase initial of each party) and exponentiate to produce a corresponding public value (uppercase initial of the party):
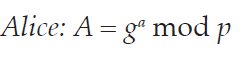
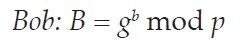
Alice and Bob exchange these two public values and they exponentiate again, using the other party’s public value as the generator to produce the shared secret:
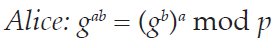
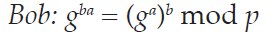
Alice and Bob now have a shared secret:
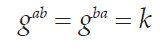
The significant property of this exchange is that the public values A and B can be exchanged over an insecure public network without reducing the security of the exchange. An eavesdropper (conventionally known as Eve) could know g and p and intercept the exchange of public values and still not be able to discover the key because one of the private values must be known to generate the shared secret.
The Diffie-Hellman exchange is vulnerable to a man-in-the-middle attack in which Mallory impersonates Bob to Alice and Alice to Bob. Both Alice and Bob believe they are performing a key exchange with one another, but in reality are doing so withMallory. When Alice sends secured data to Bob, Mallory can intercept the traffic and decrypt it before passing the packets on to Bob. Neither Alice nor Bob would notice anything out of the ordinary. This type of attack may be thwarted if Alice and Bob both digitally sign their public values.